关键路径法是项目管理中一种重要的进度计划工具，通过计算关键路径，可以明确项目的最短完成时间，识别关键活动，并为项目管理提供决策依据。

一、关键路径的定义

关键路径(Critical Path)是项目管理中用于确定项目最短完成时间的一种方法。它是指项目中一系列相互依赖的活动，这些活动的总持续时间决定了整个项目的最短完成时间。关键路径上的任何活动延迟都会直接导致项目总工期的延长。

二、关键路径的计算步骤

活动清单与依赖关系

列出项目中的所有活动(任务)。

明确每个活动的前置活动(依赖关系)，即哪些活动必须先完成才能开始当前活动。

绘制网络图

使用前导图法(PDM)或箭线图法(ADM)绘制项目网络图。

前导图法(PDM)使用节点表示活动，箭头表示依赖关系。

箭线图法(ADM)使用箭头表示活动，节点表示事件(开始或结束)。

估算活动持续时间

对每个活动估算其持续时间(工期)，通常以天、周或月为单位。

计算活动的最早开始时间(ES)和最早完成时间(EF)

最早开始时间(ES)：活动可以开始的最早时间。

对于第一个活动，ES = 0.

对于其他活动，ES = 前置活动的EF的最大值。

最早完成时间(EF)：活动可以完成的最早时间。

EF = ES + 活动持续时间。

计算活动的最晚开始时间(LS)和最晚完成时间(LF)

最晚完成时间(LF)：活动必须完成的最晚时间，以确保项目按时完成。

对于最后一个活动，LF = 项目的总工期(即关键路径的总持续时间)。

对于其他活动，LF = 后置活动的LS的最小值。

最晚开始时间(LS)：活动必须开始的最晚时间。

LS = LF - 活动持续时间。

计算活动的总浮动时间(TF)

总浮动时间(TF)：活动可以延迟而不影响项目总工期的最大时间。

TF = LS - ES 或 TF = LF - EF。

如果TF = 0.则该活动位于关键路径上。

确定关键路径

关键路径是项目中所有总浮动时间为0的活动组成的路径。

关键路径的总持续时间即为项目的最短完成时间。

三、关键路径计算示例

假设有一个简单的项目，包含以下活动：

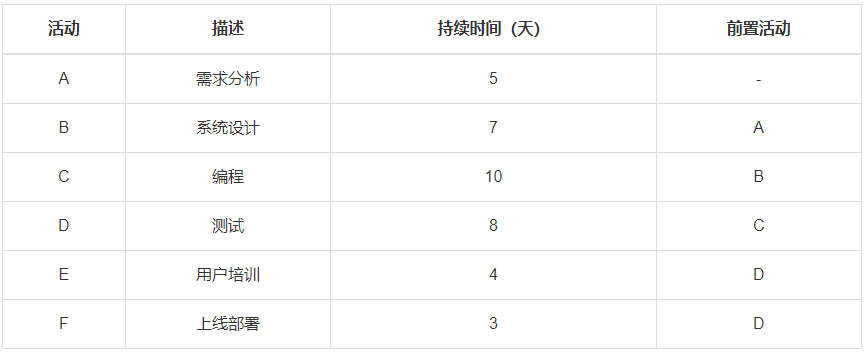
步骤1：绘制网络图

(此处为文字描述，实际应绘制图形)

A → B → C → D → E

A → B → C → D → F

步骤2：计算ES和EF

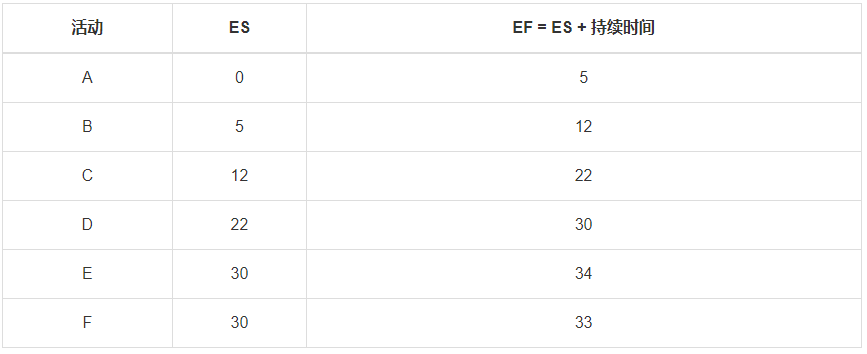
步骤3：计算LF和LS(反向计算)

项目的总工期为34天(E的EF)。

从后向前计算：

步骤4：计算TF

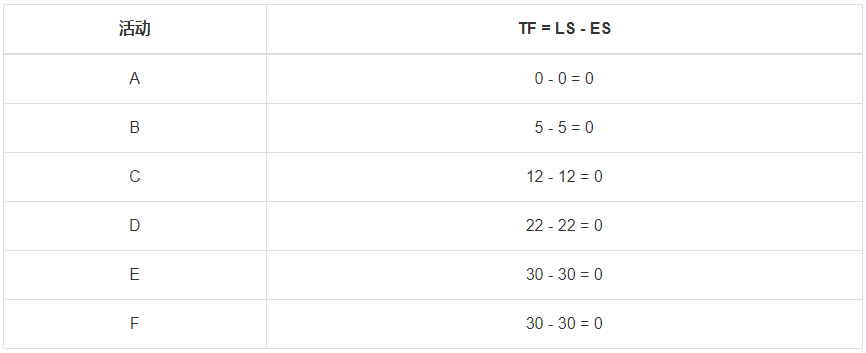
步骤5：确定关键路径

所有活动的TF均为0.因此关键路径为：A → B → C → D → E 和 A → B → C → D → F。

项目的最短完成时间为34天(由E决定)。

四、关键路径法的注意事项

多条关键路径

一个项目可能有多条关键路径，这意味着这些路径上的活动都需要严格管理，以确保项目按时完成。

浮动时间的使用

非关键路径上的活动具有一定的浮动时间，可以在不影响项目总工期的情况下进行灵活调整。

关键路径的动态性

关键路径可能会随着项目的进展而发生变化。例如，如果某条非关键路径上的活动延迟时间超过了其浮动时间，可能会成为新的关键路径。

资源约束

关键路径法假设资源是无限的，但在实际项目中，资源可能是有限的。此时，可能需要结合资源平衡技术来优化项目进度。

五、关键路径法的优势

明确项目工期：通过计算关键路径，可以明确项目的最短完成时间。

识别关键活动：关键路径上的活动是项目管理的重点，需要特别关注。

优化项目进度：通过分析浮动时间，可以合理安排资源，优化项目进度。

六、关键路径法的局限性

假设资源无限：未考虑资源约束，可能导致计划不可行。

静态分析：未考虑活动持续时间的不确定性，可能低估项目风险。

复杂性：对于大型项目，网络图可能非常复杂，计算量大。